Gradien Descent
The aim of a neural network is, to minimize the cost function calculated on its parameters, which, if using the same network as in ML-10, are:
\[\begin{align} & W^{[1]} \in \mathbb{R}^{(n^{[1]}, n^{[0]})} \\ & b^{[1]} \in \mathbb{R}^{(n^{[1]}, 1)} \\ & W^{[2]} \in \mathbb{R}^{(n^{[2]}, n^{[1]})} \\ & b^{[2]} \in \mathbb{R}^{(n^{[2]}, 1)} \end{align}\]The cost function ($J$) is defined as the average over the training examples of the loss function ($\mathcal{L}$) for a single example:
\[J(W^{[1]},b^{[1]}, W^{[2]}, b^{[2]}) = \frac{1}{m} \sum_{i=1}^m \mathcal{L}\left(\hat{y}, y \right)\]where, if the network is used for binary classification, $\mathcal{L}$ can be exactly the same as in logistic regression.
In order to train the network, we will need to perform gradient descent, so:
-
For each iteration until convergence:
- compute the prediciton $\hat{y}$
- compute the derivatives $\frac{\partial J}{\partial W^{[1]}}, \frac{\partial J}{\partial b^{[1]}},\frac{\partial J}{\partial W^{[2]}}, \frac{\partial J}{\partial b^{[2]}}$
- update the parameters $W^{[1]}=W^{[1]}-\alpha \frac{\partial J}{\partial W^{[1]}},\cdots$
Backpropagation
In order to compute the derivatives in a neural network, we use a technique called backpropagation, where we proceed step by step backwards in the computation of the contribution to $J$ from weights of the different layers from the rightmost to the leftmost taking advantage of the chain rule.
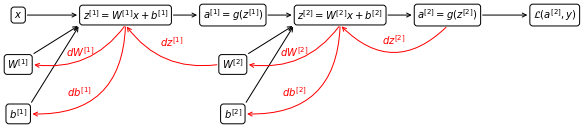
The derivative $dW^{[2]}= \frac{\partial J}{\partial W^{[2]}}$ and $db^{[2]}= \frac{\partial J}{\partial b^{[2]}}$ are esaily calculated in two steps:
\[\begin{aligned} &dZ^{[2]}=A^{[2]} - Y\\ &dW^{[2]}= \frac{1}{m}dZ^{[2]}A^{[1]T}\\ &db^{[2]}= \frac{1}{m}\sum dZ^{[2]} \end{aligned}\]We can see that in order to calculate $dW^{[2]}$ and $db^{[2]}$, we need to calculate the term $dZ^{[2]}$, that represents the error a layer.
To calculate $dW^{[1]}$ and $db^{[1]}$, we need $dZ^{[2]}$, which is calculated building on the the calculation in the previous layer
\[\begin{aligned} &dZ^{[1]}= W^{[2]T} dZ^{[2]} \odot g' (Z^{[1]})\\ &dW^{[1]}= \frac{1}{m}dZ^{[2]}\\ &db^{[1]}= \frac{1}{m}\sum dZ^{[1]} \end{aligned}\]