Mini-batch gradient descent

When training a deep-learning model, you training set might be create some problems at training.

For example the MNIST training set consists of 60000 images. Training an algorithm on the whole dataset would:

• require a lot of memory
• cumulate the rounding errors
• slow down training

In order to prevent this problems, the training set is usually split in mini-batches. For example you might split a 5,000,000 examples training set in 1,000 mini-batches ($t$) of 5,000 training examples each. You would have 1,000 feature vectors $X^{{t}}, Y^{{t}}$.

From here you would proceed by iterating over your 1000 mini-batches in each training epoch. Below you can see some pseudocode representing the process, where I focus on epoch and mini-batches and remain less rigorous on layers:

iteration = 0
for epoch in range(n_epochs):         # number of epochs
    for t in range(n_minibatches):    # 1000 mini-batches of size 5000 each
        iteration += 1
        a = forward_prop(w, x[t], b)
        J[t] = compute_cost(a, y[t])
        dw = backprop(x[t], y[t])
        w := update_weigths(dw)

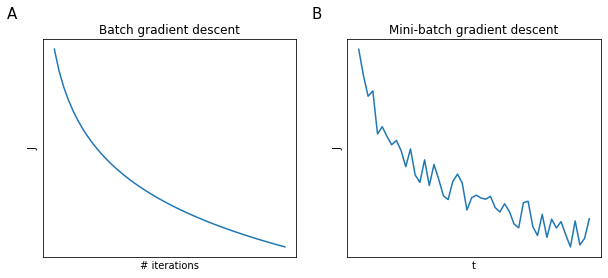
Whereas in batches you expect the value of the cost function $J$ to monotonically decrease with the number of iterations and if this doesn’t happen is a signal of some error in the implementation of gradient descent, in mini-batch gradient descent for each $t$ we could have a local increase or decrease f $J$, depending on how hard the examples in the mini-batch are. There should still be a trend down at the increase of $t$ (Figure 60).

Size of mini-batch

The size of the mini-batch ($m_b$) is an hyperparameter that you will need to chose.

• If $m_b=m$ we have classic batch gradient descent where $(X^{{1}}, Y^{{1}}) = (X, Y)$. Batch gradient descent will bring our cost function steadily towards the minimum and to convergence.

• If $m_b=1$ we have an algorithm called stochastic gradient descent where every example is its own mini-batch $(X^{{1}}, Y^{{1}}) = (x^{(1)}, y^{(1)})$. Stochastic gradient descent will bring on average our cost function towards the minimum but with many detours and will never converge.

• In practice $1 < m_b < m$. This will ensure the fastest learning. Typical mini-batches sizes are power of 2, that tend to run faster due to computer architectural implementations. Usually these sizes are used: $64, 128, 256, 512$.

Nomenclature

The introduction mini-batches and epochs creates ambiguity in some terminology. To disambiguate, especially in deep-learning

• The dataset of size $m$ is split in $b$ mini-batches of size $m_b$
• Each iteration an algorithm visits a mini-batch
• Each epoch an algorithm visits the entire dataset (all mini-batches)

When $m_b=m$ (batch gradient descent) the definition of iteration and epoch coincides, this is beacuse sometimes we will find epochs referred to as iterations.

Comments